Matriks Matematika : Pengertian, Notasi, Ordo, Transpose, dan Kesamaan Dua Matriks

 

alvininfo.com - Hello Gaes !!! Kembali lagi bersama admin ganteng alvininfo.com, kali ini saya akan membahas materi matriks matematika. Kalian pasti udah ngga asing dong dengan matriks, banyak banget manfaat dari matriks ini dalam kehidupan nyata. 

Berikut contoh manfaat penerapan matriks dalam kehidupan nyata atau sehari-hari :

• Matriks banyak dimanfaatkan untuk menyelesaikan berbagai permasalahan matematika seperti menemukan solusi masalah persamaan linear
• Membuat model sebuah permasalahan di bidang ekonomi
• Membuat model sebuah permasalahan di bidang pendidikan
• Penyelesaian dalam masalah jual beli

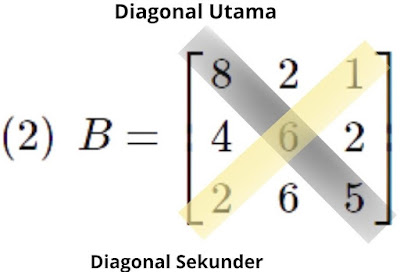
Pengertian Matriks

Matriks adalah kumpulan bilangan, simbol, atau ekspresi, berbentuk persegi atau persegi panjang yang disusun menurut baris dan kolom. 

Contoh Matriks

Penjelasan Tambahan :

1. Matriks tanda kurung biasa
2. Matriks tanda kurung siku

Notasi Matriks

Matriks dinyatakan dengan huruf kapital dan elemen-elemennya dinyatakan dengan huruf non kapital. Jika \(A\) adalah matriks, \(a_{ij}\) menyatakan elemen yang terletak pada baris ke-i dan kolom ke-j.

Contoh Notasi Matriks 

\[A=\left[ \begin{matrix} 3&5&6 \\ 1&4&-9 \\ 8&7&7\\ \end{matrix}\right]\]

Elemen pada baris ke-3 kolom ke-2 \(=a_{32}=7\)

Elemen pada baris ke-1 kolom ke-3 \(=a_{13}=6\)

Ordo Matriks 

Jika suatu matriks \(A\) terdiri dari \(m\) baris dan \(n\) kolom, maka \(m\times n\) menyatakan ukuran atau ordo dari matriks \(A\).

Contoh Ordo Matriks

Tentukan ordo dari matriks di bawah ini :

\(1) \hspace{4mm}X=\left[\begin{matrix}2&3&4\\4&1&-2\end{matrix}\right]\)

\(2) \hspace{4mm}Y=\left[\begin{matrix}5\\4\\3\end{matrix}\right]\)

Pembahasan 

1) Ordo matriks \(X\) adalah \(2\times3\) ditulis \(X_{2\times3}\)

2) Ordo matriks \(Y\) adalah \(3\times1\) ditulis \(Y_{3\times1}\)

Jenis-jenis Matriks

Jenis-jenis matriks dikelompokkan menjadi tiga, yang pertama berdasarkan banyak baris dan kolom, yang kedua berdasarkan pola elemen-elemen dan yang ketiga berdasarkan nilai determinannya.

Jenis-jenis Matriks Berdasarkan Banyak Baris dan Kolom

Matriks baris

Matriks baris adalah matriks yang hanya terdiri dari satu baris saja tidak peduli sebanyak apapun kolomnya. 

Contoh matriks baris seperti di bawah ini :

\((1)\hspace{2mm}X=\left[\begin{matrix}1&2&2\end{matrix}\right]\)

\((2)\hspace{2mm}Y=\left[\begin{matrix}1&2&2&5\end{matrix}\right]\)

\((3)\hspace{2mm}Z=\left[\begin{matrix}4&5\end{matrix}\right]\)

Matriks kolom

Matriks kolom adalah matriks yang hanya terdiri dari satu kolom saja tidak peduli sebanyak apapun barisnya. 

Contoh matriks kolom seperti di bawah ini :

\((1)\hspace{2mm}A=\left[\begin{matrix}2\\3\\2\end{matrix}\right]\)

\((2)\hspace{2mm}B=\left[\begin{matrix}4\\3\\2\\8\end{matrix}\right]\)

\((3)\hspace{2mm}C=\left[\begin{matrix}9\\7\end{matrix}\right]\)

Matriks persegi panjang

Matriks persegi panjang adalah matriks yang memiliki jumlah baris dan kolom berbeda. 

Contoh matriks persegi panjang seperti di bawah ini :

\((1)\hspace{2mm}A=\left[\begin{matrix}2&5\\3&6\\2&8\end{matrix}\right]\)

\((2)\hspace{2mm}B=\left[\begin{matrix}4&2&1\\4&6&2\end{matrix}\right]\)

Matriks persegi

Matriks persegi adalah matriks yang memiliki jumlah baris dan kolom yang sama. 

Contoh matriks persegi seperti di bawah ini :

Penjelasan Tambahan :

1. Matriks Persegi Ordo \(2\times2\)
2. Matriks Persegi Ordo \(3\times3\)

Hasil penjumlahan diagonal utama disebut dengan trace.

1. Trace matriks nomor \(1\) adalah \(11\), diperoleh dari \(3+8\)
2. Trace matriks nomor \(2\) adalah \(19\), diperoleh dari \(8+6+5\)

Jenis-jenis Matriks Berdasarkan Pola Elemen-Elemen

Matriks nol \((O)\)

Matriks nol adalah matriks yang semua elemennya memiliki nilai nol. 

Contoh matriks nol seperti di bawah ini :

\(O_{2\times3}=\left[\begin{matrix}0&0&0\\0&0&0\end{matrix}\right]\)

\(O_{2\times2}=\left[\begin{matrix}0&0\\0&0\end{matrix}\right]\)

Matriks diagonal \((D)\)

Matriks diagonal adalah matriks persegi dengan elemen pada diagonal utamanya tidak semua nol sementara elemen lainnya nol. 

Berikut contoh matriks diagonal :

\(D_{3\times3}=\left[\begin{matrix}1&0&0\\0&2&0\\0&0&1\end{matrix}\right]\)

\(D_{3\times3}=\left[\begin{matrix}3&0&0\\0&0&0\\0&0&0\end{matrix}\right]\)

Matriks identitas \((I)\)

Matriks identitas adalah matriks persegi dengan semua elemen pada diagonal utamanya bernilai \(1\) sedangkan elemen lainnya nol.

\(I_{3\times3}=\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\end{matrix}\right]\)

\(I_{2\times2}=\left[\begin{matrix}1&0\\0&1\end{matrix}\right]\)

Matriks segitiga

Matriks segitiga adalah matriks persegi dengan elemen-elemen di bawah atau di atas diagonal utamanya bernilai nol semua. 

Matriks segitiga terdiri dari matriks segitiga atas dan segitiga bawah. 

• Matriks segitiga atas \((U)\)

Matriks segitiga atas adalah matriks yang semua elemen di bawah diagonal utamanya bernilai nol. 

Contoh matriks segitiga atas seperti di bawah ini :

\(U_{3\times3}=\left[\begin{matrix}1&2&3\\0&1&2\\0&0&2\end{matrix}\right]\)

• Matriks segitiga bawah \((L)\)

Matriks segitiga bawah adalah matriks yang semua elemen di atas diagonal utamanya bernilai nol. 

Contoh matriks segitiga bawah seperti di bawah ini :

\(L_{3\times3}=\left[\begin{matrix}1&0&0\\2&1&0\\1&2&2\end{matrix}\right]\)

Jenis-jenis Matriks Berdasarkan Nilai Determinannya

1. Matriks singular adalah matriks yang nilai determinannya nol, \(\left|A\right|=0\)
2. Matriks nonsingular adalah matriks yang nilai determinannya tidak sama dengan nol, \(\left|A\right|\neq0\)

Transpose Matriks

Transpose matriks merupakan sebuah matriks yang disusun dengan cara menukar elemen pada baris menjadi elemen pada kolom atau sebaliknya. Matriks \(A\) transpose disimbolkan dengan \(A^{T}\).

Contoh Transpose Matriks 

Contoh 1

\(A=\left[\begin{matrix}2&4&6\\3&2&1\\5&9&4\end{matrix}\right]\) transpose dari matriks \(A \hspace{1mm}\Rightarrow A^{T}=\left[\begin{matrix}2&3&5\\4&2&9\\6&1&4\end{matrix}\right]\).

Contoh 2

\(B=\left[\begin{matrix}3&2&5\\2&5&6\\5&6&7\end{matrix}\right]\) transpose dari matriks \(B \hspace{1mm}\Rightarrow B^{T}=\left[\begin{matrix}3&2&5\\2&5&6\\5&6&7\end{matrix}\right]\).

Penjelasan Tambahan :

Pada contoh 2 matriks \(B\) dan \(B^{T}\) memiliki elemen yang sama. Kasus ini dinamakan matriks simetris karena \(B=B^{T}\).

Kesamaan Dua Matriks

Kesamaan dua matriks yaitu dua matriks yang memiliki ordo dan elemen-elemen seletak yang sama. Contoh kesamaan dua matriks seperti di bawah ini :

Diketahui matriks \(A=\left[\begin{matrix}1&2\\3&7^{2}\end{matrix}\right]\) dan matriks \(B=\left[\begin{matrix}tan\frac{\pi}{4}&2\\\sqrt{9}&49\end{matrix}\right]\)

Penjelasan :

Nilai \(1\) sama dengan nilai \(tan\frac{\pi}{4}\) karena nilai dari \(tan\hspace{1mm}30^{\circ}\) adalah \(1\). Begitu juga dengan \(3=\sqrt{9}\) dan \(7^{2}=49\).

Operasi Matriks

Dalam matriks, ada banyak operasi yang bisa dilakukan. Beberapa operasi telah kita kenal sebelumnya, jenis-jenis operasi matriks lainnya yang berkaitan, yaitu :

1. Operasi penjumlahan matriks
2. Operasi pengurangan matriks
3. Operasi perkalian skalar dengan matriks 
4. Operasi perkalian matriks dengan matriks

Operasi Penjumlahan Matriks

Cara menjumlahkan dua matriks atau lebih yaitu dengan menjumlahkan elemen atau entri yang seletak. Perlu diingat! kedua matriks bisa dijumlahkan apabila memiliki baris dan kolom yang sama. 

Biar lebih jelas perhatikan contoh di bawah ini:

Contoh penjumlahan matriks

\(\left(\begin{matrix}2&8\\1&9\\3&8\end{matrix}\right)+\left(\begin{matrix}5&2\\3&4\\7&6\end{matrix}\right)=\left(\begin{matrix}7&10\\4&13\\10&14\end{matrix}\right)\)

Operasi Pengurangan Matriks

Cara melakukan pengurangan matriks sama aja dengan penjumlahan matriks yaitu dengan mengoperasikan yang posisinya sama atau seletak. Pengurangan matriks juga hanya dapat dilakukan apabila memiliki jumlah baris dan kolom yang sama. 

Untuk lebih jelas perhatikan contoh di bawah ini.

Contoh pengurangan matriks

\(\left(\begin{matrix}2&8\\1&-9\\3&-8\end{matrix}\right)-\left(\begin{matrix}5&2\\3&-4\\7&-6\end{matrix}\right)\\=\left(\begin{matrix}-3&6\\-2&-5\\-4&-2\end{matrix}\right)\)

Operasi Perkalian Skalar dengan Matriks

Dalam operasi matriks, skalar dapat kita maknai sebagai sembarang nilai bilangan real. 

Notasi dari perkalian matriks dengan skalar adalah :

Contoh perkalian skalar dengan matriks

Jika \(B=\left(\begin{matrix}2&3&-4\\7&6&0\end{matrix}\right)\) tentukan matriks \(4B\)

Pembahasan

\(4B= 4\left(\begin{matrix}2&3&-4\\7&6&0\end{matrix}\right)\)

\(4B= \left(\begin{matrix}8&12&-16\\28&24&0\end{matrix}\right)\)

Operasi Perkalian Matriks dengan Matriks

Misal diketahui matriks \(A_{m\times n}\) dan matriks \(B_{n\times p}\). Perkalian matriks \(A\) dan \(B\) akan menghasilkan matriks baru yang berordo \(m\times p\). 

Gampangnya perkalian matriks dengan matriks dapat dilakukan apabila jumlah kolom dan baris antara kedua matriks sama. 

Jadi, ditulis \(A_{m\times n}\times B_{n\times p}=(AB)_{m\times p}\). Untuk lebih jelasnya perhatikan contoh di bawah ini.

Contoh perkalian matriks dengan matriks

Jika matriks \(A=\left(\begin{matrix}4&2\\3&7\\0&2\end{matrix}\right)\) dan \(B=\left(\begin{matrix}-1&0&1\\5&4&2\end{matrix}\right)\) dan \(C=A\times B\). Tentukan matriks \(C\)...

Pembahasan

Ordo matriks \(A\) adalah \(3\times2\) dan ordo matriks \(B\) adalah \(2\times3\). Karena matriks \(A\) memiliki \(2\) kolom dan matriks \(B\) memiliki \(2\) baris, maka kedua matriks tersebut dapat dilakukan operasi perkalian matriks dengan matriks sesuai \(A_{3\times 2}\times B_{2\times 3}=(AB)_{3\times 3}\).

Cara melakukan perkalian matriks dengan matriks yaitu mangalikan baris dari matriks \(A\) dengan kolom matriks \(B\).

\(C=A\times B\)

\(C=\left(\begin{matrix}4&2\\3&7\\0&2\end{matrix}\right) \times \left(\begin{matrix}-1&0&1\\5&4&2\end{matrix}\right)\)

\(C=\left(\begin{matrix}-4+10&0+8&4+4\\-3+35&0+28&3+14\\0+10&0+8&0+4\end{matrix}\right)\)

\(C=\left(\begin{matrix}6&8&8\\32&28&17\\10&8&4\end{matrix}\right)\)

Determinan Matriks

Salah satu tanda pengenal dari suatu matriks adalah determinannya. Definisi dari determinan sendiri yaitu suatu faktor yang menentukan (determine) sesuatu. 

Dalam matriks, determinan ini sendiri berupa suatu bilangan yang dihitung untuk suatu matriks persegi atau gampangnya determinan matriks itu hanya terdapat pada matriks persegi.

Determinan matriks dapat ditulis seperti gambar di bawah ini :

Determinan Matriks Berordo \(2\times2\)

Cara menghitung determinan matriks ordo \(2\times2\) yaitu hasil kali diagonal utama dikurangi dengan hasil kali diagonal sekunder. 

Jika \(A=\left(\begin{matrix}a&b\\c&d\end{matrix}\right)\) maka det\(A=\left|A\right|=ad-bc\).

Contoh determinan matriks ordo \(2\times2\)

Diketahui \(A=\left(\begin{matrix}4&5\\7&8\end{matrix}\right)\). Tentukan determinan dari matriks \(A\) ....

Pembahasan

\(\left|A\right|=(4\times8)-(5\times7)\)

\(\left|A\right|=32-35\)

\(\left|A\right|=-3\)

Determinan Matriks Berordo \(3\times3\)

Cara menghitung determinan matriks ordo \(3\times3\) ada dua cara. 

Yang pertama menggunakan metode sarrus dan yang kedua menggunakan metode kofaktor atau ekspansi laplace.

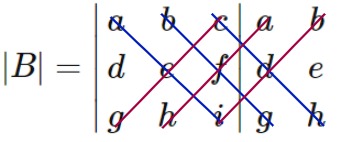
Cara menghitung determinan matriks ordo 3x3 menggunakan metode sarrus

Misal diketahui matriks \(B=\left(\begin{matrix}a&b&c\\d&e&f\\g&h&i\end{matrix}\right)\) maka cara mencari determinan matriksnya dengan menggunakan metode sarrus seperti di bawah ini :

Langkah 1

Tambahkan dua kolom yaitu kolom \(1\) dan kolom \(2\) di samping matriks \(B\).

\(\left|B\right|=\left|\begin{matrix}a&b&c\\d&e&f\\g&h&i\end{matrix}\right|\begin{matrix}a&b\\d&e\\g&h\end{matrix}\)

Langkah 2

Selanjutnya, hasil penjumlahan dari perkalian semua diagonal utama dikurangi dengan semua penjumlahan dari perkalian semua diagonal sekunder.

\(=aei+bfg+cdh-(ceg+afh+bdi)\)

Cara menghitung determinan matriks ordo 3x3 menggunakan metode kofaktor

Cara mudah menentukan determinan matriks ordo \(3\times3\) dengan menggunakan metode kofaktor atau ekspansi laplace, caranya seperti di bawah ini.

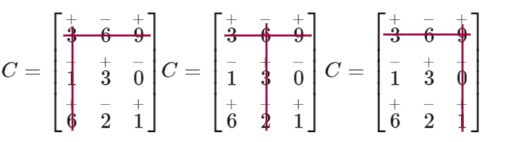
Misal diketahui ada matriks \(C\) lalu tentukan determinannya menggunakan metode kofaktor...

\(C=\left[\begin{matrix}3&6&9\\1&3&0\\6&2&1\end{matrix}\right]\)

Langkah 1

Kalian buat tanda \(+\) dan \(-\) selang seling pada setiap elemen matriks seperti di bawah ini :

\(C=\left[\begin{matrix}\overset{+}{3}&\overset{-}{6}&\overset{+}{9}\\\overset{-}{1}&\overset{+}{3}&\overset{-}{0}\\\overset{+}{6}&\overset{-}{2}&\overset{+}{1}\end{matrix}\right]\)

Tambahan informasi, tanda \(+\) dan \(-\) digunakan sebagai operasi perkalian terhadap elemen\entri pada baris atau kolom yang dipilih untuk menjadi angka acuan di depan matriks ordo \(2\times2\).

Langkah 2

Selanjutnya tentukan baris atau kolom manapun dengan bebas sesuka hati tanpa ada paksaan dan aturan. 

Baris atau kolom yang sudah dipilih akan digunakan sebagai angka di depan matriks ordo \(2\times2\). Lebih jelasnya perhatikan penjelasan di bawah ini.

Perlu diketahui ekspansi ini memecah matriks menjadi ordo \(2\times2\), jika saya memilih baris pertama untuk digunakan sebagai angka di depan matriks ordo \(2\times2\) maka akan diperoleh untuk matriks ordo \(2\times2\) nya seperti gambar di bawah ini :

\(C=3\left[\begin{matrix}3&0\\2&1\end{matrix}\right]-6\left[\begin{matrix}1&0\\6&1\end{matrix}\right]+9\left[\begin{matrix}1&3\\6&2\end{matrix}\right]\)

\(C=3(3-0)-6(1-0)+9(2-18)\)

\(C=3(3)-6(1)+9(-16)\)

\(C=9-6-144\)

\(C=-141\)

Jadi determinan dari matriks \(C\) adalah \(-141\). Agar lebih yakin kalian bisa mencoba menghitung determinan dari matriks \(C\) dengan menggunakan metode sarrus pasti hasilnya sama saja.

Contoh determinan matriks ordo \(3\times3\)

Tentukan determinan dari matriks ordo \(3\times3\) di bawah ini :

\(D=\left[\begin{matrix}1&-2&3\\5&2&3\\4&1&0\end{matrix}\right]\)

Pembahasan

Metode sarrus

\(D = (1\times2\times0) + (-2\times3\times4)\\+(3\times5\times1)-(3\times2\times4)\\-(1\times3\times1)-(-2\times5\times0)\)

\(D = (0) + (-24)+(15)\\-(24)-(3)-(0)\)

\(D = 0 -24+15-24-3-0\)

\(D = 15-51\)

\(D=-36\)

Metode Kofaktor

\(D=\left[\begin{matrix}\overset{+}{1}&\overset{-}{-2}&\overset{+}{3}\\\overset{-}{5}&\overset{+}{2}&\overset{-}{3}\\\overset{+}{4}&\overset{-}{1}&\overset{+}{0}\end{matrix}\right]\)

Langkah 1

Saya menggunakan baris pertama sebagai angka acuan atau angka di depan matriks ordo \(2\times2\). Maka diperoleh angka acuannya yaitu \(1,-2\) dan \(3\).

Langkah 2

Karena sudah ada contoh sebelumnya mengenai cara mencari determinan ordo \(3\times3\) menggunakan metode kofaktor maka sekarang saya tidak menjelaskan tahapannya, disini saya akan langsung menghitungnya saja.

\(D=1\left|\begin{matrix}2&3\\1&0\end{matrix}\right|-(-2)\left|\begin{matrix}5&3\\4&0\end{matrix}\right|+3\left|\begin{matrix}5&2\\4&1\end{matrix}\right|\)

\(D=1(0-3)+2(0-12)+3(5-8)\)

\(D=1(-3)+2(-12)+3(-3)\)

\(D=-3-24-9\)

\(D=-36\)

Jadi determinan dari matriks \(D\) dengan menggunakan metode kofaktor adalah \(-36\). Sama saja hasilnya dengan metode sarrus. 

Sifat-sifat Determinan Matriks

• \(\left|A^{T}\right|=\left|A\right|\)
• \(\left|A^{-1}\right|=\frac{1}{\left|A\right|}\)
• \(\left|AB\right|=\left|A\right|.\left|B\right|\)
• \(\left|A^{n}\right|=\left|A\right|^{n}\)
• \(\left|k.A\right|=k^{n}.\left|A\right|\) dengan \(n\) adalah ordo matriks

Minor, Kofaktor, dan Adjoin Matriks

Materi minor, kofaktor dan adjoin matriks memiliki keterkaitan antara satu dengan yang lainnya atau saling berhubungan. 

Jadi kalian harus paham materi minor matriks sebelum mempelajari materi kofaktor matriks agar memudahkan kalian dalam mempelajari materi adjoin matriks. 

Materi ini dipake untuk mencari invers matriks dan determinan matriks khusunya minor dan kofaktor. 

Minor Matriks

Jika \(a_{ij}\) adalah elemen matriks \(A\) yang terletak pada baris ke\(-i\) dan kolom ke \(-j\), maka minor dari \(a_{ij}\) yang dinyatakan oleh \(M_{ij}\) adalah determinan/bilangan tunggal setelah baris ke\(-i\) dan kolom ke\(-j\) di hilangkan.

Contoh minor matriks

Tentukan minor dari matriks ordo \(2\times2\) dan ordo \(3\times3\) di bawah ini :

Matriks \(A=\left[\begin{matrix}1&2\\3&4\end{matrix}\right]\) dan matriks \(B=\left[\begin{matrix}2&3&2\\3&4&3\\1&5&6\end{matrix}\right]\)......

Pembahasan

1. Mencari minor dari matriks \(A\)

Perlu diketahui karena matriks \(A\) adalah matriks ordo \(2\times2\), jadi setelah baris ke\(-i\) dan kolom ke\(-j\) dihilangkan maka yang tersisa hanya bilangan tunggal.

\(M_{11}=4\)

\(M_{12}=3\)

\(M_{21}=2\)

\(M_{22}=1\)

Jadi minor dari matriks \(A\) adalah \(M_{A}=\left[\begin{matrix}M_{11}&M_{12}\\M_{21}&M_{22}\end{matrix}\right]=\left[\begin{matrix}4&3\\2&1\end{matrix}\right]\)

2. Mencari minor dari matriks \(B\)

Karena matriks \(B\) adalah ordo \(3\times3\) jadi setelah salah satu baris dan kolomnya dihilangkan maka yang tersisa adalah matriks ordo \(2\times2\). 

Jadi untuk mendapatkan minor dari matriks \(B\) maka kalian perlu mencari nilai determinan dari matriks ordo \(2\times2\).

\(M_{11}=\left|\begin{matrix}4&3\\5&6\end{matrix}\right|=24-15=9\)

\(M_{12}=\left|\begin{matrix}3&3\\1&6\end{matrix}\right|=18-3=15\)

\(M_{13}=\left|\begin{matrix}3&4\\1&5\end{matrix}\right|=15-4=11\)

\(M_{21}=\left|\begin{matrix}3&2\\5&6\end{matrix}\right|=18-10=8\)

\(M_{22}=\left|\begin{matrix}2&2\\1&6\end{matrix}\right|=12-2=10\)

\(M_{23}=\left|\begin{matrix}2&3\\1&5\end{matrix}\right|=10-3=7\)

\(M_{31}=\left|\begin{matrix}3&2\\4&3\end{matrix}\right|=9-8=1\)

\(M_{32}=\left|\begin{matrix}2&2\\3&3\end{matrix}\right|=6-6=0\)

\(M_{33}=\left|\begin{matrix}3&2\\4&3\end{matrix}\right|=8-9=-1\)

Jadi minor matriks \(B\) adalah \(M_B=\left[\begin{matrix}M_{11}&M_{12}&M_{13}\\M_{21}&M_{22}&M_{23}\\M_{31}&M_{32}&M_{33}\end{matrix}\right]\\=\left[\begin{matrix}9&15&11\\8&10&7\\1&0&-1\end{matrix}\right]\)

Kofaktor Matriks

Jika \(A\) adalah matriks, \(M_{ij}\) adalah minor elemen matriks \(A\) pada baris ke-\(i\) dan kolom ke-\(j\). 

Maka kofaktor \(a_{ij}\) yang dinyatakan \(K_{ij}\) adalah minor \(M_{ij}\) setelah diberi \((-1)^{i+j}\). 

\[K_{ij}=(-1)^{i+j}.M_{ij}\]

Untuk menentukan kofaktor dari suatu matriks kalian harus mencari minor dari matriksnya terlebih dahulu. Kofaktor hanya perkalian tanda \(+\) atau \(-\) dengan minor elemen matriks.

Contoh Kofaktor Matriks

Tentukan kofaktor dari matriks \(B=\left[\begin{matrix}2&3&2\\3&4&3\\1&5&6\end{matrix}\right]\) adalah...

Pembahasan

Karena matriks \(B\) sudah dicari minornya pada contoh minor matriks, selanjutnya kalian hanya tinggal memberi tanda \(+\) dan \(-\) selang seling. 

Maka diperoleh kofaktor dari matriks \(B\) seperti di bawah ini. 

\(K_B=\left[\begin{matrix}9&-15&11\\-8&10&-7\\1&0&-1\end{matrix}\right]\)

Pemberian tanda \(+\) dan \(-\) tersebut diperoleh dari rumus di bawah ini.

\(K_{11}=(-1)^{1+1}.M_{11}\)

\(K_{11}=(-1)^{2}.9\)

\(K_{11}=9\)

\(K_{12}=(-1)^{1+2}.M_{12}\)

\(K_{12}=(-1)^{3}.15\)

\(K_{12}=-15\)

\(K_{13}=(-1)^{1+3}.M_{13}\)

\(K_{13}=(-1)^{4}.11\)

\(K_{13}=11\)

\(K_{21}=(-1)^{2+1}.M_{21}\)

\(K_{21}=(-1)^{3}.8\)

\(K_{21}=-8\)

\(K_{22}=(-1)^{2+2}.M_{22}\)

\(K_{22}=(-1)^{4}.10\)

\(K_{22}=10\)

\(K_{23}=(-1)^{2+1}.M_{23}\)

\(K_{23}=(-1)^{3}.7\)

\(K_{23}=-7\)

\(K_{31}=(-1)^{3+1}.M_{31}\)

\(K_{31}=(-1)^{4}.1\)

\(K_{31}=1\)

\(K_{32}=(-1)^{3+2}.M_{32}\)

\(K_{32}=(-1)^{5}.0\)

\(K_{32}=0\)

\(K_{33}=(-1)^{3+3}.M_{33}\)

\(K_{33}=(-1)^{6}.-1\)

\(K_{33}=-1\)

Adjoin Matriks

Cara mencari adjoin matriks yaitu dengan mentrasposkan kofaktor dari matriks tersebut.

\[Adj(A)=(kof(A))^{T}\]

Contoh adjoin matriks

Tentukan adjoin dari matriks \(B=\left[\begin{matrix}2&3&2\\3&4&3\\1&5&6\end{matrix}\right]\).....

Pembahasan

Karena matriks \(B\) sudah didapatkan kofaktornya maka selanjutnya tinggal transposekan saja.

\(K_B=\left[\begin{matrix}9&-15&11\\-8&10&-7\\1&0&-1\end{matrix}\right]\)

\((K_B)^{T}=\left[\begin{matrix}9&-8&1\\-15&10&0\\11&-7&-1\end{matrix}\right]\)

Invers Matriks 

Invers matriks adalah dua matriks persegi yang berordo sama dan saling invers atau berkebalikan jika memenuhi hubungan \(AB=BA=I \). Simbol dari invers matriks adalah pangkat \(-1\) di atas hurufnya.

Rumus invers matriks :

\[A^{-1}=\frac{1}{det(A)}. Adj (A)\]

Sifat-sifat Invers Matriks

• \(AB=C\leftrightarrow A=CB^{-1}\)
• \(AB=C\leftrightarrow B=A^{-1}C\)
• \(AA^{-1}=A^{-1}A=I\)
• \((A^{-1})^{-1}=A\)
• \((AB)^{-1}=B^{-1}A^{-1}\)

Invers Matriks 2x2

Tentukan invers dari matriks \(A=\left[\begin{matrix}2&4\\1&3\end{matrix}\right]\) adalah...

Pembahasan

Mencari adjoin matriks \(A\)

Misal diketahui matriks ordo 2x2, \(X=\left[\begin{matrix}a&b\\c&d\end{matrix}\right]\) maka adjoinnya adalah \(Adj(X)=\left[\begin{matrix}d&-b\\-c&a\end{matrix}\right]\). 

Maka adjoin dari matriks \(A\) adalah \(Adj(A)=\left[\begin{matrix}3&-4\\-1&2\end{matrix}\right]\)

Mencari determinan matriks \(A\) 

\(\left|A\right|= (2\times3)-(4\times1)\)

\(\left|A\right|= 6-4=2\)

Mencari invers matriks \(A\)

\(A^{-1}=\frac{1}{2}\left[\begin{matrix}3&-4\\-1&2\end{matrix}\right]\)

\(A^{-1}=\left[\begin{matrix}\frac{3}{2}&-2\\\frac{-1}{2}&1\end{matrix}\right]\)

Invers Matriks 3x3

Diketahui matriks \(A=\left[\begin{matrix}3&2&1\\4&-2&5\\3&3&1\end{matrix}\right]\). Tentukan invers matriks \(A\).....

Pembahasan

Cara menyelesaikan matriks \(A\) invers ordo \(3\times3\).

• Mencari determinan

\(A=\left[\begin{matrix}3&2&1\\4&-2&5\\3&3&1\end{matrix}\right]\)

\(\left|A\right|=3\left[\begin{matrix}-2&5\\3&1\end{matrix}\right]-2\left[\begin{matrix}4&5\\3&1\end{matrix}\right]\\+1\left[\begin{matrix}4&-2\\3&3\end{matrix}\right]\)

\(\left|A\right|=3(-2-15)-2(4-15)\\+1(12-(-6))\)

\(\left|A\right|=3(-17)-2(-11)+1(18)\)

\(\left|A\right|=-51+22+1(18)\)

\(\left|A\right|=-11\)

• Mencari adjoin matriks

Minor matriks \(A\)

\(M_{11}=-17 \hspace{5mm}M_{12}=-11\hspace{5mm}M_{13}=18\)

\(M_{21}=-1\hspace{5mm}M_{22}=0\hspace{5mm}M_{23}=3\)

\(M_{31}=12\hspace{5mm}M_{32}=11\hspace{5mm}M_{33}=-14\)

Kofaktor matriks \(A\)

\(D=\left[\begin{matrix}\overset{+}{-17}&\overset{-}{-11}&\overset{+}{18}\\\overset{-}{-1}&\overset{+}{0}&\overset{-}{3}\\\overset{+}{12}&\overset{-}{11}&\overset{+}{-14}\end{matrix}\right]\\=\left[\begin{matrix}-17&11&18\\1&0&-3\\12&-11&-14\end{matrix}\right]\)

Adjoin matriks \(A\)

Adjoin = Transpose dari kofaktor, jadi untuk mencari adjoin tinggal transposekan kofaktor matriks \(A\)

\((kof(A))^{T}=\left[\begin{matrix}-17&1&12\\11&0&-11\\18&-3&-14\end{matrix}\right]\)

• Invers matriks \(A\)

\(A^{-1}=\frac{1}{Determinan}\hspace{1mm}Adjoin\)

\(A^{-1}=\frac{1}{-11}\left[\begin{matrix}-17&1&12\\11&0&-11\\18&-3&-14\end{matrix}\right]\)

Contoh Soal Matriks

Soal 1

Diketahui persamaan matriks 

\(3\left(\begin{matrix}4&1\\6&b\end{matrix}\right)+\left(\begin{matrix}3a&5\\1&4\end{matrix}\right)\\=\left(\begin{matrix}2&1\\5&4\end{matrix}\right)\left(\begin{matrix}3&2\\1&4\end{matrix}\right)\)

Nilai dari \(3a+3b\) adalah....

Pembahasan

\(\left(\begin{matrix}12&3\\18&3b\end{matrix}\right)+\left(\begin{matrix}3a&5\\1&4\end{matrix}\right)=\left(\begin{matrix}7&8\\19&26\end{matrix}\right)\)

Diperoleh persamaan matriks :

\(12+3a=7\)

\(3a=7-12=-5\)

\(3b+4=26\)

\(3b=26-4=22\)

\(3a+3b=-5+22=17\)

Soal 2

Diketahui matriks \(A=\left(\begin{matrix}4&3\\2&2\end{matrix}\right)\), \(B=\left(\begin{matrix}-5&4\\-2&4\end{matrix}\right)\), jika \(AX=B\). Tentukan matriks \(X\).....

Pembahasan

\(AX=B\)

\(X=A^{-1}B\)

\(A^{-1}=\frac{1}{2}\left[\begin{matrix}2&-3\\-2&4\end{matrix}\right]\)

\(A^{-1}=\left[\begin{matrix}1&\frac{-3}{2}\\-1&2\end{matrix}\right]\)

\(X=A^{-1}B\)

\(X=\left[\begin{matrix}1&\frac{-3}{2}\\-1&2\end{matrix}\right]\left[\begin{matrix}-5&4\\-2&4\end{matrix}\right]\)

\(X=\left[\begin{matrix}-2&-2\\1&4\end{matrix}\right]\)

Penutup

Sekian pembahasan materi matriks matematika, apabila ada yang tidak jelas silahkan ditanyakan.