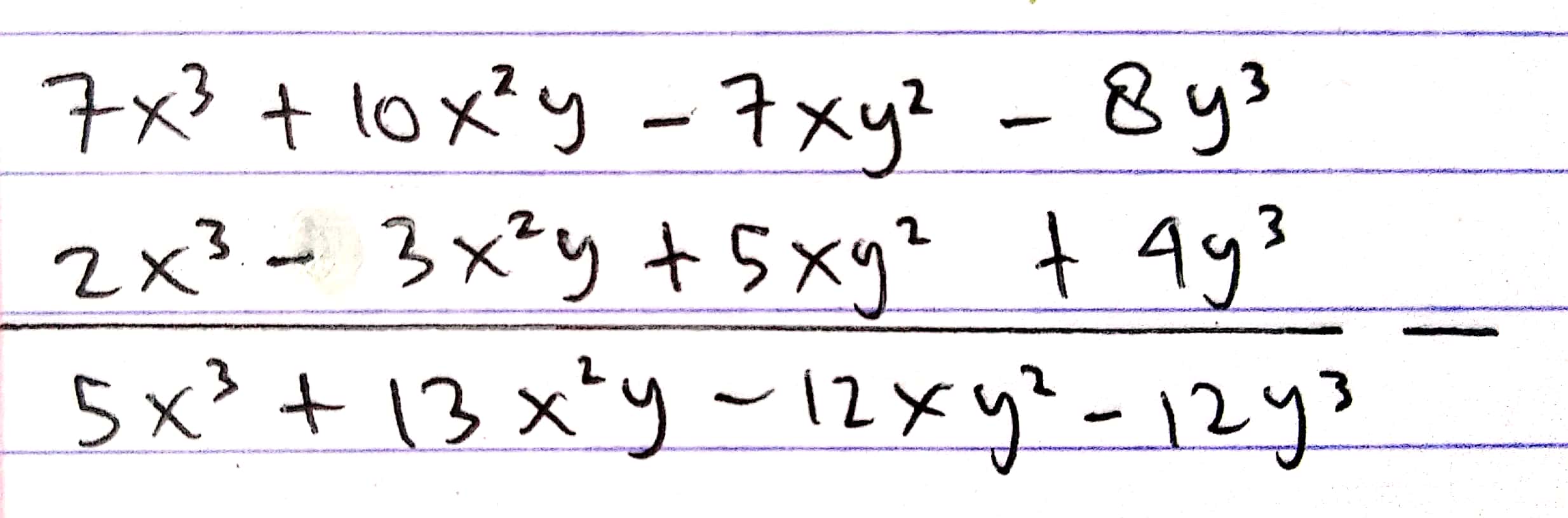alvininfo.com - Aljabar adalah suatu ilmu dalam matematika yang mempelajari simbol dan bagaimana memanipulasi simbol tersebut. \(\alpha\) (alpha), \(\beta\) (beta) dan \(\gamma\) (gamma) adalah simbol yunani yang termasuk simbol-simbol aljabar. Bentuk aljabar terdiri dari suku, variabel dan koefisien.
Baca Juga : Materi Aljabar Olimpiade Matematika SMA
Suku adalah gabungan antara variabel dengan koefisien. Variabel adalah huruf di belakang koefisien. Koefisien adalah angka di depan variabel. Biar makin paham mengenai suku, variabel, dan koefisien. Pelajari contoh di bawah ini :
Contoh Bentuk Aljabar
Tentukan suku, variabel dan koefisien dari bentuk aljabar berikut \(-4a^{2}b^{3}+7a^{3}+6b^{2}-5ab^{2}-1\) !!
Pembahasan
1. Suku dalam bentuk aljabar dipisahkan oleh tanda \(+\) atau \(-\) di depan koefisien bukan di belakang variabel.
- \(-4a^{2}b^{3}\)
- \(7a^{3}\)
- \(6b^{2}\)
- \(-5ab^{2}\)
- \(-1\)
2. Variabel
- \(a^{2}b^{3}\)
- \(a^{3}\)
- \(b^{2}\)
- \(ab^{2}\)
- \(a^{0}\)
3. Koefisien
- \(-4\)
- \(7\)
- \(6\)
- \(-5\)
- \(-1\)
Pada contoh soal di atas ada satu koefisien yang memiliki variabel berpangkat nol \(0\) yaitu \(-1\). Angka \(-1\) ini dinamakan konstanta karena nilainya tidak berubah. Kenapa ga berubah ? karena semua variabel yang berpangkat \(0\) jika dioperasikan nilainya satu.
Pokoknya konstanta itu koefisien yang variabelnya berpangkat nol. Biasanya di soal langsung ditulis angka saja tanpa variabel pangkat nol.
Tambahan, dalam menyusun aljabar ada dua ketentuan yang pertama diurutkan berdasarkan variabel dan yang kedua diurutkan berdasarkan pangkat.
Langkah pertama untuk menyusunnya, urutkan dulu variabel sesuai urutan huruf abjad a-z setelah variabel nya sesuai urutan a-z selanjutnya mengurutkan pangkat dari yang terbesar sampai yang terkecil.
Contoh
\(ab^{2}+ab^{3}+c^{3}+a^{3}+a^{2}c^{3}+b^{4}\) \(\Rightarrow\) urutan yang salah
\(a^{3}+a^{2}c^{3}+ab^{3}+ab^{2}+b^{4}+c^{3}\) \(\Rightarrow\) urutan yang benar
Baca Juga : Contoh Soal Model Matematika
Operasi Hitung Bentuk Aljabar Penjumlahan dan Pengurangan
Penjumlahan dan pengurangan bentuk aljabar bisa dioperasikan jika ada dua suku aljabar yang sejenis ( pangkat dan variabelnya sama ).
Contoh Soal Pengurangan Bentuk Aljabar dan Pembahasannya
\(1.\) \(3a-2a= a\) atau \(1a\)
\(2.\) \(4a-4a=0\)
\(3.\) \(5b-3a= \) \(\Rightarrow\)Tidak bisa dioperasikan karena variabelnya berbeda
\(4.\) \(7a-3b+8a-9b=15a-12b\)
\(5.\) \(4x^{2}-3x=\) \(\Rightarrow\)Tidak bisa dioperasikan karena pangkatnya berbeda
\(6.\) \(3x^{2}-4x+7x-8x^{2}= -5x^{2}+3x\)
Contoh Soal Pengurangan Bentuk Aljabar Bersusun
Dengan menyusun ke bawah, tentukan :
Soal Nomor 1
\(5p^{5}-5p^{3}-8p^{2}\) dikurangi dengan \(8p^{5}-5p^{4}+3p^{3}-10p\)
Soal Nomor 2
\(7x^{3}+10x^{2}y-7xy^{2}-8y^{3}\) dikurangi dengan \(2x^{3}+5xy^{2}-3x^{2}y+4y^{3}\)
Pembahasan
Pembahasan Soal Nomor 1
Pembahasan Soal Nomor 2
Soal Pengurangan Bentuk Aljabar
Soal Nomor 1
\((8x^{3}+12x^{2}y-5xy^{2}-5y^{3})\\-(3x^{3}-xy^{2}-5x^{2}y+11y^{3})=\)
Soal Nomor 2
\((-8x^{3}+14xy^{2}+7x^{2}y)-\\(8x^{3}+12x^{2}y-5xy^{2}-5y^{3})=\)
Soal Nomor 3
\((4a^{2}-4a+7)-(5a^{3}-6a^{2}+7a)=\)
Soal Nomor 4
\(-(4x^{3}+3x^{2}y-6xy^{2}+5y^{3})-\\(-6x^{2}-2xy^{2}+8y^{3})=\)
Soal Nomor 5
\(5y+4-(-7x+3-(4x-1)+5x)\\-(2x+1-(x-6y)-7)=\)
Pembahasan
Pembahasan Soal Nomor 1
\((8x^{3}+12x^{2}y-5xy^{2}-5y^{3})\\-(3x^{3}-xy^{2}-5x^{2}y+11y^{3})=\)
\(8x^{3}+12x^{2}y-5xy^{2}-5y^{3}\\-3x^{3}+xy^{2}+5x^{2}y-11y^{3}=\)
\(8x^{3}-3x^{3}+12x^{2}y+5x^{2}y\)\(+xy^{2}-5xy^{2}-11y^{3}-5y^{3}= \)
\(5x^{3}+17x^{2}y-4xy^{2}-16y^{3}\)
Pembahasan Soal Nomor 2
\((-8x^{3}+14xy^{2}+7x^{2}y)-\\(8x^{3}+12x^{2}y-5xy^{2}-5y^{3})=\)
\(-8x^{3}+14xy^{2}+7x^{2}y\\-8x^{3}-12x^{2}y+5xy^{2}+5y^{3}=\)
\(-8x^{3}-8x^{3}+7x^{2}y-12x^{2}y\\+5xy^{2}+14xy^{2}+5y^{3}=\)
\(-16x^{3}-5x^{2}y+19xy^{2}+5y^{3}\)
Pembahasan Soal Nomor 3
\((4a^{2}-4a+7)-(5a^{3}-6a^{2}+7a)=\)
\(4a^{2}-4a+7-5a^{3}+6a^{2}-7a=\)
\(-5a^{3}-4a^{2}+6a^{2}-4a-7a+7=\)
\(-5a^{3}+2a^{2}-11a+7\)
Pembahasan Soal Nomor 4
\(-(4x^{3}+3x^{2}y-6xy^{2}+5y^{3})-\\(-6x^{2}-2xy^{2}+8y^{3})=\)
\(-4x^{3}-3x^{2}y+6xy^{2}-5y^{3}+\\6x^{2}+2xy^{2}-8y^{3}=\)
\(-4x^{3}+6x^{2}-3x^{2}y+\\2xy^{2}+6xy^{2}-8y^{3}-5y^{3}=\)
\(-4x^{3}+6x^{2}-3x^{2}y+\\8xy^{2}-13y^{3}\)
Pembahasan Soal Nomor 5
\(5y+4-(-7x+3-(4x-1)+5x)-\\(2x+1-(x-6y)-7)=\)
\(5y+4-(-7x+3-4x+1+5x)-\\(2x+1-x+6y-7)=\)
\(5y+4+7x-3+4x-1-5x\\(-2x-1+x-6y+7)=\)
\(7x+4x-5x-2x+x\\-6y+5y+7+4-1-3-1=\)
\(5x-1y+6\)
Contoh Soal Penjumlahan Bentuk Aljabar dan Pembahasannya
\(1.\) \(b+b=2b\)
\(2.\) \(4b+3b=7b\)
\(3.\) \(7b+8c=\)\(\Rightarrow\) Tidak bisa dijumlahkan karena variabelnya berbeda
\(4.\) \(9b+1c+2b+5c=11b+6c\)
\(5.\) \(y+y^{2}+y^{3}=\)\(\Rightarrow\) Tidak bisa dijumlahkan karena pangkatnya berbeda
\(6.\) \(y+3y^{2}+5y+9y^{3}+4y^{2}+7y^{3}=\\6y+7y^{2}+16y^{3}\)
Contoh Soal Penjumlahan Bentuk Aljabar Bersusun dan Pembahasannya
Dengan menyusun ke bawah, jumlahkan :
Soal Nomor 1
\(4p^{5}-4p^{3}-7p^{2}\) dan \(9p^{5}-5p^{4}+6p^{3}-15p\)
Soal Nomor 2
\(-5x^{3}+3x^{2}y+4xy^{2}-8y^{3}\); \(4x^{3}-2xy^{2}+7y^{3}\) dan \(5x^{2}y-11y^{3}\)
Pembahasan
Pembahasan Soal Nomor 1
Pembahasan Soal Nomor 2
Soal Penjumlahan Bentuk Aljabar dan Pembahasannya
Soal Nomor 1
\(5x^{2}+3xy+2y^{2}+4x^{2}+4xy+6y^{2}=\)
Soal Nomor 2
Soal Nomor 2
\((-3x^{3}+6xy^{2}+8y^{3})\\+(7x^{2}y+8xy^{2}-5y^{3})\\+(8x^{3}+12x^{2}y-5xy^{2}-5y^{3})=\)
Soal Nomor 3
\((3a+4ab+6b)+(-7a+12ab-10b)=\)
Pembahasan
Pembahasan Soal Nomor 1
\(5x^{2}+3xy+2y^{2}+4x^{2}+4xy+6y^{2}=\)
\(5x^{2}+4x^{2}+3xy+4xy+2y^{2}+6y^{2}=\)
\(9x^{2}+7xy+8y^{2}\)
Pembahasan Soal Nomor 2
\((-3x^{3}+6xy^{2}+8y^{3})\\+(7x^{2}y+8xy^{2}-5y^{3})\\+(8x^{3}+12x^{2}y-5xy^{2}-5y^{3})=\)
\(-3x^{3}+6xy^{2}+8y^{3}\\+7x^{2}y+8xy^{2}-5y^{3}\\+8x^{3}+12x^{2}y-5xy^{2}-5y^{3}=\)
\(-3x^{3}+8x^{3}+7x^{2}y+12x^{2}y\\+8xy^{2}+6xy^{2}-5xy^{2}\\-5y^{3}+8y^{3}-5y^{3}=\)
\(5x^{3}+19x^{2}y+9xy^{2}+8y^{3}\)
Pembahasan Soal Nomor 3
\((3a+4ab+6b)+(-7a+12ab-10b)=\)
\(3a-7a+4ab+12ab+6b-10b=\)
\(-4a+16ab-4b\)
Operasi Hitung Bentuk Aljabar Perkalian
Dua suku aljabar dapat dikalikan, bagaimanapun bentuknya selalu bisa dikalikan. Dalam perkalian aljabar berlaku rumus berikut \(A^{x}\times A^{y}=A^{x+y}\). Untuk perkalian bentuk aljabar, jika variabelnya sama maka pangkatnya bisa dijumlahkan.
Tips perkalian bentuk aljabar :
- Kalikan dulu angkanya
- Kalikan variabelnya, jika variabelnya sama maka pangkatnya dijumlahkan
Contoh Soal Operasi Hitung Bentuk Aljabar Perkalian
- \(a\times a=a^{2}\)
- \(3a \times 2a=6a^{2}\)
- \(2b \times 4a=8ab\)
- \(4a \times 3b=12ab\)
- \(7x^{2}\times 2x=14x^{3}\)
- \(6x^{2}y\times 2xy^{2}=12x^{3}y^{3}\)
Soal Perkalian Aljabar dan Pembahasannya
Soal Nomor 1
\(4(x-3)(x+1(-2x+5)-6)=\)
Soal Nomor 2
\(2a^{2}b(5a^{3}b^{2}-6a^{3}bc^{2}+10c^{5})\\-4c^{3}(8a^{3}b^{2}-5a^{3}bc^{2}-8c^{5})=\)
Soal Nomor 3
\((-2x^{2}y-z)(2xy^{2}+5xyz)=\)
Pembahasan
Pembahasan Soal Nomor 1
\(4(x-3)(x+1(-2x+5)-6)=\)
\((4x-12)(-x-1)=\)
\(-4x^{2}-4x+12x+12=\)
\(-4x^{2}+8x+12\)
Pembahasan Soal Nomor 2
\(2a^{2}b(5a^{3}b^{2}-6a^{3}bc^{2}+10c^{5})\\-4c^{3}(8a^{3}b^{2}-5a^{3}bc^{2}-8c^{5})=\)
\(10a^{5}b^{3}-12a^{5}b^{2}c^{2}+20a^{2}bc^{5}\\-32a^{3}b^{2}c^{3}+20a^{3}bc^{5}+32c^{8}\)
\(10a^{5}b^{3}-12a^{5}b^{2}c^{2}-32a^{3}b^{2}c^{3}+20a^{3}bc^{5}\\+20a^{2}bc^{5}+32c^{8}\)
👆
Hasil yang sudah disusun berdasarkan ketentuan penyusunan aljabar.
Pembahasan Soal Nomor 3
\((-2x^{2}y-z)(2xy^{2}+5xyz)=\)
\(-4x^{3}y^{3}-10x^{3}y^{2}z-2xy^{2}z-5xyz^{2}\)
Operasi Hitung Bentuk Aljabar Pembagian
Dalam pembagian aljabar, berlaku rumus berikut \(A^{x}:A^{y}=A^{x-y}\). Untuk pembagian bentuk aljabar hanya tinggal mengurangkan pangkatnya saja tetapi variabelnya harus sama. Jika variabelnya berbeda maka pangkatnya tidak bisa dikurang.
Contoh Operasi Hitung Bentuk Aljabar Pembagian
1. \(a^{5}:a^{3}=a^{5-3}=a^{2}\)
2. \(18a^{4}:9a^{3}=\frac{18}{9}a^{4-3}=2a\)
3. \(-64a^{4}b^{3}:16a^{2}b=\frac{-64}{16}a^{4-2}b^{3-1}=-4a^{2}b^{2}\)
Soal Pembagian Aljabar dan Pembahasannya
Untuk mempermudah dalam mengerjakan soal pembagian aljabar bisa mulai dengan mengoperasikan perkalian tanda positif dan negatif (Rumus Perkalian Bilangan Bulat) jika ada, lalu kelompokan suku yang memiliki variabel sama. Setelah itu operasikan pembagian aljabar pada variabel yang sama.
Soal Nomor 1
\(-(6a^{3}x^{3}-12a^{4}x^{3}+a^{3}x^{2}) : 3a^{2}x=\)
Soal Nomor 2
\(\frac{27a^{2}b+12ab^{3}-21a^{2}b^{2}}{3ab}=\)
Pembahasan
Pembahasan Soal Nomor 1
\(-(6a^{3}x^{3}-12a^{4}x^{3}+a^{3}x^{2}) : 3a^{2}x=\)
\(-6a^{3}x^{3}+12a^{4}x^{3}-a^{3}x^{2} : 3a^{2}x=\)
\(-2ax^{2}+4a^{2}x^{2}-\frac{1}{3}ax\)
Pembahasan Soal Nomor 2
\(\frac{27a^{2}b+12ab^{3}-21a^{2}b^{2}}{3ab}=\)
\(\frac{27}{3}a^{2-1}b^{1-1}+\frac{12}{3}a^{1-1}b^{3-1}-\frac{21}{3}a^{2-1}b^{2-1}=\)
\(9a+4b^{2}-7ab\)
Sederhanakan Bentuk Bentuk Aljabar Berikut
Sederhanakan bentuk bentuk aljabar berikut menggunakan operasi hitung perkalian, pembagian, penjumlahan dan pengurangan bentuk aljabar
Soal Nomor 1
\(5a+2a-10=\)
Soal Nomor 2
\(9p+8q+5p-2q=\)
Soal Nomor 3
\(7m^{2}+8m+6-10m^{2}-2m-10=\)
Soal Nomor 4
\(8(2x^{2}+4x)-20x^{2}=\)
Soal Nomor 5
\(8a-9b-6c+(-10a+9b+12c)=\)
Soal Nomor 6
\( 5x(3x^{2}-6x+8)+2x(3x^{2}+6x-8)=\)
Soal Nomor 7
\(\frac{6a}{4x}-\frac{4}{2x}=\)
Soal Nomor 8
\(\frac{2x}{6x} \times \frac{x-4}{6x}=\)
Soal Nomor 9
\(\frac{x^{2}y^{2}}{2z} : \frac{18xy}{6}=\)
Soal Nomor 10
\(\frac{3b-bx}{cx-3c}=\)
Pembahasan
Pembahasan Nomor 1
\(5a+2a-10=7a-10\)
Pembahasan Nomor 2
\(9p+8q+5p-2q=14p+6q\)
Pembahasan Nomor 3
\(7m^{2}+8m+6-10m^{2}-2m-10=\)
\(-3m^{2}+6m-4\)
Pembahasan Nomor 4
\(8(2x^{2}+4x)-20x^{2}=\)
\(16x^{2}+32x-20x^{2}= -4x^{2}+32x\)
Pembahasan Nomor 5
\(8a-9b-6c+(-10a+9b+12c)=\)
\(8a-9b-6c-10a+9b+12c=-2a+6c\)
Pembahasan Nomor 6
\( 5x(3x^{2}-6x+8)+2x(3x^{2}+6x-8)=\)
\( 15x^{3}-30x^{2}+40x+6x^{3}+12x^{2}-16x=\)
\( 15x^{3}+6x^{3}-30x^{2}+12x^{2}+40x-16x=\)
\(21x^{3}-18x^{2}+24x\)
Pembahasan Nomor 7
\(\frac{6a}{4x}-\frac{4}{2x}=\)
\(\frac{6a \times 2x - 4 \times 4x}{4x \times 2x}= \frac{12ax-16x}{8x^{2}}\)
Pembahasan Nomor 8
\(\frac{2x}{6x} \times \frac{x-4}{6x}=\)
\(\frac{2x\times (x-4)}{6x \times 6x }=\frac{2x^{2}-8x}{36x^{2}}\)
Pembahasan Nomor 9
\(\frac{x^{2}y^{2}}{2z} : \frac{18xy}{6}=\)
Perlu diingat !
Pembagian adalah kebalikan dari perkalian, contohnya \(\frac{2}{\frac{1}{2}}=2 \times\frac{2}{1}\).
Nah soal nomer 9 juga sama bisa dimisalkan seperti ini.
\(\frac{x^{2}y^{2}}{2z} : \frac{18xy}{6}= \frac{x^{2}y^{2}}{2z} \times \frac{6}{18xy}=\)
\(\frac{6x^{2}y^{2}}{36xyz}\)
Pembahasan Nomor 10
\(\frac{3b-bx}{cx-3c}=\)
\(\frac{b(3-x)}{-c(3-x)}=\frac{b}{-c}\)