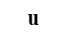Materi Vektor Matematika PDF - Materi konsep dasar vektor
meliputi besaran skalar, besaran vektor, cara menggambarkan vektor dan notasi
vektor.
Besaran skalar merupakan besaran yang hanya mempunyai nilai saja dan tidak mempunyai arah, contoh besaran skalar yaitu jarak, luas, volume, daya dan kelajuan.
Besaran vektor merupakan besaran yang mempunyai nilai dan arah, contohnya
seperti perpindahan, kecepatan, percepatan dan gaya.
Baca Juga : Persamaan Logaritma Kelas 10
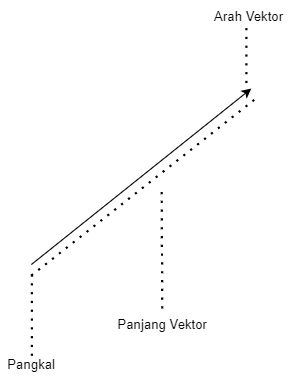
Cara Menggambarkan Vektor
Penjelasan dari gambar di atas :
Vektor digambarkan dengan sebuah anak panah yang terdiri dari pangkal yang
menandakan titik awal atau titik tangkap sebuah vektor, panjang vektor
yang merepresentasikan besar atau nilai suatu vektor, dan arah anak panah
adalah ujung vektornya yang menunjukan arah vektor.
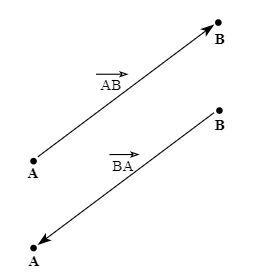
Notasi Vektor
Untuk gambar anak panah yang pertama atau paling atas merepresentasikan vektor
\(\vec{AB}\) karena titik pangkal sebuah vektornya di A dan
ujung vektornya di B.
Sedangkan untuk gambar anak panah paling bawah atau yang kedua
merepresentasikan vektor \(\vec{BA}\) karena titik pangkal atau
awal sebuah vektornya di B dan arah anak panah atau ujung vektornya di
A.
Pokoknya \(\overrightarrow{AB}\) adalah vektor A menuju B sedangkan
\(\overrightarrow{BA}\) adalah vektor B menuju A. Jika kalian memperhatikan
penulisannya, itu dimulai dengan titik pangkal dulu kemudian ujung vektornya.
Penggunaan vektor bisa juga menggunakan huruf non kapital yang
diberikan tanda panah di atasnya, atau di bawah hurufnya diberikan garis dan
bisa juga dengan menebalkan huruf nya. Untuk semua contoh penulisannya
berurutan sesuai yang saya terangkan di kalimat sebelumnya.
Contoh :
Vektor pada Bidang \((R_2)\)
Vektor pada bidang hanya memiliki dua dimensi diantaranya yaitu kiri-kanan
(horizontal) dan atas-bawah (vertikal). Sehingga hanya memiliki dua sumbu
yaitu sumbu \(x\) dan sumbu \(y\).
\( a = \left(\begin{matrix}x\\y\end{matrix}\right)\)
- \(x\) = Merepresentasikan arah panah pada garis horizontal, jika arah panahnya ke kanan maka nilainya positif \((+)\) sedangkan jika arah panahnya ke kiri maka nilainya negatif \((-)\).
- \(y\) = Merepresentasikan arah panah pada garis vertikal, jika arah panahnya ke atas maka nilainya positif \((+)\) sedangkan jika arah panahnya ke bawah maka nilainya negatif \((-)\).
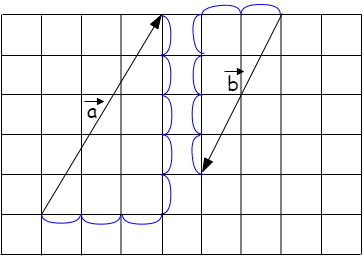
Contoh gambar vektor pada bidang
Mungkin untuk lebih jelas perhatikan contoh di bawah ini :
- Angka \(3\) didapat dari. Tiga langkah dari titik pangkal menuju titik perpotongan antara garis horizontal dengan vertikal, karena arah dari titik pangkal menuju titik perpotongan ke kanan maka nilainya positif.
- Angka \(5\) didapat dari. Lima langkah dari titik perpotongan antara garis horizontal dengan vertikal menuju arah vektor/panah, karena arah vektornya ke atas maka nilainya positif.
Vektor \(b\) bisa ditulis menjadi
\(b=\left(\begin{matrix}-2\\-4\end{matrix}\right)\) atau bisa juga ditulis
\(\vec{b}=(-2,-4)\) dan \(\vec{b}=-2i-4j\).
- Angka \(-2\) didapat dari. Dua langkah dari titik pangkal menuju titik perpotongan antara garis horizontal dengan vertikal, karena arah dari titik pangkal menuju titik perpotongan ke kiri maka nilainya negatif.
- Angka \(-4\) didapat dari. Empat langkah dari titik perpotongan antara garis horizontal dengan vertikal menuju arah vektor/panah, karena arah vektornya ke bawah maka nilainya negatif.
Vektor pada Ruang \((R_3)\)
Untuk menggambarkan vektor pada ruang cukup sulit karena vektor ruang
memiliki tiga dimensi diantaranya yaitu depan-belakang, kanan-kiri, dan
atas-bawah. Jadi vektor pada ruang memiliki tiga sumbu yaitu \(x\),
\(y\), dan \(z\).
- Sumbu \(x\) merepresentasikan dimensi depan-belakang.
- Sumbu \(y\) merepresentasikan dimensi kanan-kiri.
- Sumbu \(z\) merepresentasikan dimensi atas-bawah.
Untuk memudahkan kalian dalam memahami cara menggambarkan vektor pada
ruang, silahkan perhatikan contohnya di bawah ini :
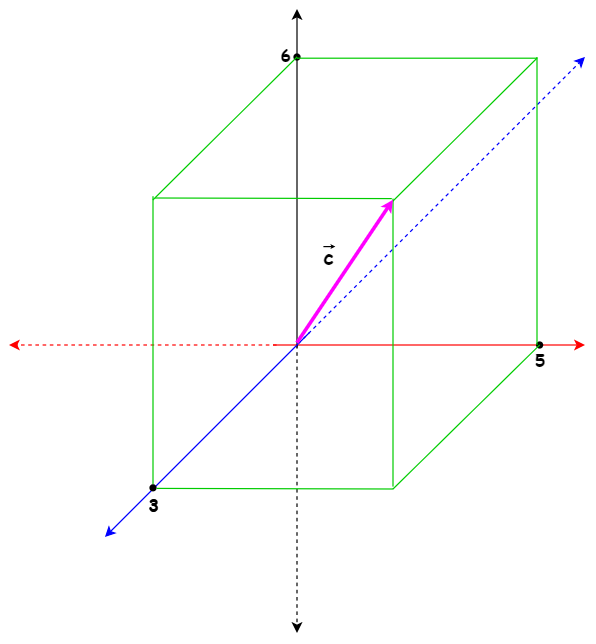
Cara menggambar vektor pada ruang
Gambarkan vektor
\(\vec{c}=\left(\begin{matrix}3\\5\\6\end{matrix}\right)\)
Pembahasan
Langkah 1 :
- Membuat gambar garis panah sumbu \(x\) ( warna biru ), sumbu \(y\) ( warna merah ), dan sumbu \(z\) ( warna hitam ). Untuk garis panah putus-putus merupakan wilayah untuk vektor yang bernilai negatif ( belakang, kiri, dan bawah ).
- Cara menggambarkan vektor \(\vec{c}\) kita perlu menghubungkan titik-titik dimensi \(x\), \(y\), dan \(z\).
- Jika titik-titik tersebut sudah dihubungkan maka akan membentuk bangun ruang.
- Selanjutnya untuk menggambarkan vektor \(\vec {c}\) hanya tinggal membuat garis panah dari titik pangkal koordinat menuju ujung atau sudut kanan atas bagian depan ( notes : kalau \(y\) negatif maka sudut kiri atas bagian depan berhubung di soal ini \(y\) nya bernilai positif jadi sudut kanan atas bagian depan ).
Baca Juga : Soal dan Pembahasan Polinomial Kelas 11
Vektor Posisi
Vektor posisi adalah vektor yang titik pangkalnya 0. Vektor posisi titik
\(A\) ditulis \(\overrightarrow{OA}\) atau \(\vec{a}\).
Jika \(A\) \((x,y,z)\), maka
\(\vec{a}=\overrightarrow{OA}=\left(\begin{matrix}x\\y\\z\end{matrix}\right)\)
Panjang vektor \(\vec{a}\) adalah \(\begin{vmatrix} \vec{a} \\
\end{vmatrix}= \sqrt{x^{2}+y^{2}+z^{2}} \)
Panjang Vektor, Jarak Dua Titik dan Vektor Satuan
Penjelasan gambar di atas :
\(\overrightarrow{OP}=\ \begin{pmatrix} x \\ y \end{pmatrix}\)
Panjang vektor \(\overrightarrow{OP}\)
\(\begin{vmatrix} \overrightarrow{OP} \\ \end{vmatrix} =
\sqrt{x^{2}+y^{2}}\)
Panjang Vektor \(R_2\)
\(\vec{u}=\ \begin{pmatrix} a \\ b \end{pmatrix}\hspace{2mm}
\rightarrow\) \(\begin{vmatrix} \vec{u} \\ \end{vmatrix} =
\sqrt{a^{2}+b^{2}}\)
Panjang Vektor \(R_3\)
Jarak Dua Titik
Vektor = vektor posisi ujung - vektor posisi pangkal
\[\begin{vmatrix}\vec{AB}\end{vmatrix}=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}\]
Vektor Satuan
Vektor satuan adalah vektor yang memiliki panjang satu. Rumus vektor
satuan yang searah vektor \(\vec{v}\) adalah seperti di bawah ini:
\[\hat{e_v}=\frac{1}{\begin{vmatrix}\vec{v}\\ \end{vmatrix}}.\vec{v}\]
Contoh Soal Panjang Vektor, Jarak Dua Titik dan Vektor Satuan
Soal 1
Diketahui koordinat titik \(A\)\((-3,6)\) dan \(B\)\((8,-4)\). Tentukan
vektor \(\vec{AB}\)
Pembahasan
\(\vec{AB}= \vec{b}-\vec{a}\)
\(=\left(\begin{matrix}8\\-4\end{matrix}\right)-\left(\begin{matrix}-3\\6\end{matrix}\right)\)
\(=\left(\begin{matrix}11\\-10\end{matrix}\right)\)
Soal 2
Diketahui vektor \(\vec{a}=\left(\begin{matrix}-3\\4\end{matrix}\right)\).
Tentukan panjang vektor \(\vec{a}\)
Pembahasan
\(\begin{vmatrix}\vec{a}\end{vmatrix}= \sqrt{(-3)^{2}+(4)^{2}}\)
\(\begin{vmatrix}\vec{a}\end{vmatrix}= \sqrt{9+16}\)
\(\begin{vmatrix}\vec{a}\end{vmatrix}= \sqrt{25}\)
\(\begin{vmatrix}\vec{a}\end{vmatrix}= 5\)
Soal 3
Jika diketahui koordinat titik \(A(5,-7)\) dan \(B(-4,5)\). Berapakah
jarak antara titik \(A\) dan \(B\) (panjang vektor
\(\begin{vmatrix}AB\end{vmatrix}\) )?
Pembahasan
\(\overrightarrow{AB}=\vec{b}-\vec{a}\)
\(\overrightarrow{AB}=\left(\begin{matrix}-4\\5\end{matrix}\right)-\left(\begin{matrix}5\\-7\end{matrix}\right)\)
\(\overrightarrow{AB}=\left(\begin{matrix}-9\\12\end{matrix}\right)\)
Panjang Vektor \(\overrightarrow{AB}\)
\(\begin{vmatrix}\overrightarrow{AB}\end{vmatrix}=\sqrt{(-9)^{2}+(12)^{2}}\)
\(\begin{vmatrix}\overrightarrow{AB}\end{vmatrix}=\sqrt{81+144}\)
\(\begin{vmatrix}\overrightarrow{AB}\end{vmatrix}=\sqrt{225}\)
\(\begin{vmatrix}\overrightarrow{AB}\end{vmatrix}=15\)
Kita juga bisa mencari panjang vektor \(\overrightarrow{AB}\) menggunakan
rumus jarak dua titik. Lebih jelasnya pelajari cara di bawah ini :
\(\begin{vmatrix}\overrightarrow{AB}\end{vmatrix}=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}\)
\(\begin{vmatrix}\overrightarrow{AB}\end{vmatrix}=\sqrt{(-4-5)^{2}+(5-(-7))^{2}}\)
\(\begin{vmatrix}\overrightarrow{AB}\end{vmatrix}=\sqrt{(-9)^{2}+(12)^{2}}\)
\(\begin{vmatrix}\overrightarrow{AB}\end{vmatrix}=\sqrt{81+144}\)
\(\begin{vmatrix}\overrightarrow{AB}\end{vmatrix}=\sqrt{225}\)
\(\begin{vmatrix}\overrightarrow{AB}\end{vmatrix}=15\)
Soal 4
Diketahui vektor
\(\vec{a}=\begin{pmatrix}\frac{-3}{5}\\\frac{4}{5}\end{pmatrix}\)
dan \(\vec{b}=\begin{pmatrix}-2\\1\end{pmatrix}\). Manakah diantara
kedua vektor tersebut yang termasuk vektor satuan ?
Pembahasan
Vektor satuan adalah vektor yang memiliki panjang satu.
Mengecek panjang vektor \(\vec{a}\)
\(\begin{vmatrix}\vec{a}\end{vmatrix}=\sqrt{(\frac{-3}{5})^{2}+(\frac{4}{5})^{2}}\)
\(\begin{vmatrix}\vec{a}\end{vmatrix}=\sqrt{\frac{9}{25}+\frac{16}{25}}\)
\(\begin{vmatrix}\vec{a}\end{vmatrix}=\sqrt{\frac{25}{25}}\)
\(\begin{vmatrix}\vec{a}\end{vmatrix} = 1\)
\(\vec{a}\) adalah vektor satuan.
Mengecek panjang vektor \(\vec{b}\)
\(\begin{vmatrix}\vec{b}\end{vmatrix}=\sqrt{(-2)^{2}+(1)^{2}}\)
\(\begin{vmatrix}\vec{b}\end{vmatrix}=\sqrt{4+1}\)
\(\begin{vmatrix}\vec{b}\end{vmatrix}=\sqrt{5}\)
\(\vec{b}\) bukan vektor satuan
Soal 5
Tentukanlah vektor satuan yang searah dengan vektor
\(\vec{m}=\begin{pmatrix}12\\-9\end{pmatrix}\)
Pembahasan
\(\begin{vmatrix}\vec{m}\end{vmatrix}=\sqrt{12^{2}+(-9)^{2}}\)
\(\begin{vmatrix}\vec{m}\end{vmatrix}=\sqrt{144+ 81}\)
\(\begin{vmatrix}\vec{m}\end{vmatrix}=\sqrt{225}\)
\(\begin{vmatrix}\vec{m}\end{vmatrix}= 15 \)
\(\hat{e_v}=\frac{1}{\begin{vmatrix}\vec{v}\\ \end{vmatrix}}.\vec{v}\)
\(\hat{e_m}=\begin{pmatrix}12\\-9\end{pmatrix}\frac{1}{15}\)
\(\hat{e_m}= \begin{pmatrix}\frac{12}{15}\\
\frac{-9}{15}\end{pmatrix}\)
Operasi Vektor Secara Aljabar
Penjumlahan Vektor Secara Aljabar
Untuk penjumlahan vektor pada bidang \((R_2)\) dan vektor pada ruang
\((R_3)\) secara aljabar sama aja. Hanya berbeda unsurnya saja
karena \((R_2)\) memiliki dua sumbu \(x\) dan \(y\) sedangkan
\((R_3)\) memiliki tiga sumbu \(x\), \(y\) dan \(z\).
Untuk \(\vec{u}\) dan \(\vec{v}\) pada dimensi dua \((R_2)\)
Jika \(\vec{u}=\left(\begin{matrix}x_1\\y_1\end{matrix}\right)\) dan
\(\vec{v}=\left(\begin{matrix}x_2\\y_2\end{matrix}\right)\) maka :
\(\vec{u} + \vec{v}=
\left(\begin{matrix}x_1\\y_1\end{matrix}\right)+\left(\begin{matrix}x_2\\y_2\end{matrix}\right)=\left(\begin{matrix}x_1+x_2\\y_1+y_2\end{matrix}\right)\)
Contoh soal penjumlahan vektor secara aljabar dan pembahasannya
Diketahui vektor
\(\vec{p}=\left(\begin{matrix}6\\-3\end{matrix}\right)\)
dan \(\vec{q}=\left(\begin{matrix}4\\5\end{matrix}\right)\) dan
\(\vec{r}=\vec{p}+\vec{q}\). Tentukan vektor \(\vec{r}\)....
Pembahasan
\(\vec{r}=\vec{p}+\vec{q}= \left(\begin{matrix}6\\-3\end{matrix}\right) +
\left(\begin{matrix}4\\5\end{matrix}\right)=\left(\begin{matrix}10\\-2\end{matrix}\right)\)
Pengurangan Vektor Secara Aljabar
Untuk pengurangan vektor pada bidang \((R_2)\) dan vektor pada ruang
\((R_3)\) secara aljabar sama aja. Hanya berbeda unsurnya saja
karena \((R_2)\) memiliki dua sumbu \(x\) dan \(y\) sedangkan
\((R_3)\) memiliki tiga sumbu \(x\), \(y\) dan \(z\).
Untuk \(\vec{u}\) dan \(\vec{v}\) pada dimensi dua \((R_2)\)
Jika \(\vec{u}=\left(\begin{matrix}x_1\\y_1\end{matrix}\right)\) dan
\(\vec{v}=\left(\begin{matrix}x_2\\y_2\end{matrix}\right)\) maka :
\(\vec{u} - \vec{v}=
\left(\begin{matrix}x_1\\y_1\end{matrix}\right)-\left(\begin{matrix}x_2\\y_2\end{matrix}\right)=\left(\begin{matrix}x_1-x_2\\y_1-y_2\end{matrix}\right)\)
Contoh soal pengurangan vektor secara aljabar dan pembahasannya
Diketahui vektor
\(\vec{p}=\left(\begin{matrix}-7\\-5\end{matrix}\right)\)
dan \(\vec{q}=\left(\begin{matrix}9\\-6\end{matrix}\right)\)
dan \(\vec{r}=\vec{p}-\vec{q}\). Tentukan vektor \(\vec{r}\)....
Pembahasan
\(\vec{r}=\vec{p}-\vec{q}= \left(\begin{matrix}-7\\-5\end{matrix}\right)
-
\left(\begin{matrix}9\\-6\end{matrix}\right)=\left(\begin{matrix}-16\\1\end{matrix}\right)\)
Perkalian Skalar dengan Vektor Secara Aljabar
Secara aljabar, perkalian skalar dengan vektor caranya kalikan semua
unsur pada vektor dengan skalar.
Misal diketahui \(\vec{a} =
\left(\begin{matrix}x_1\\y_1\end{matrix}\right)\) dan \(\vec{b} =
\left(\begin{matrix}x_1\\y_1\\z_1\end{matrix}\right)\) dan skalar \(k\),
maka :
\(k\vec{a}= \left(\begin{matrix}kx_1\\ky_1\end{matrix}\right)\) dan
\(k\vec{b}= \left(\begin{matrix}kx_1\\ky_1\\kz_1\end{matrix}\right)\)
Contoh soal perkalian skalar dengan vektor secara aljabar dan pembahasannya
Diketahui \(\vec{p}=\left(\begin{matrix}-4\\6\end{matrix}\right)\).
Tentukan vektor \(4\vec{p}\).....
Pembahasan
\(4\vec{p}=4\left(\begin{matrix}-4\\6\end{matrix}\right)=\left(\begin{matrix}-16\\24\end{matrix}\right)\)
Kesamaan Vektor
Dua buah vektor atau lebih dikatakan sama jika vektor-vektor tersebut
memiliki
arah dan panjang yang sama.
Secara Geometri
Secara geometris vektor dikatakan sama jika besar atau panjang dan
arahnya sama.
- \(\vec{AB}=\vec{CD}\) karena arah dan panjangnya sama.
- \(\vec{AB}\neq\vec{FE}\) karena arahnya beda walaupun panjangnya sama.
- \(\vec{EF}=-\vec{FE}\) karena jika di depan vektor diberi tanda negatif maka arahnya menjadi berbalik arah atau berlawanan dari arah vektor yang sesungguhnya. Analogi gampangnya \(1=-(-1)\).
Secara Aljabar
Secara aljabar vektor dikatakan sama jika unsur-unsur yang bersesuaian
sama. Misal diketahui vektor
\(\vec{a}=\left(\begin{matrix}a_1\\a_2\\a_3\end{matrix}\right)\) dan
\(\vec{b}=\left(\begin{matrix}b_1\\b_2\\b_3\end{matrix}\right)\). Jika
\(\vec{a}=\vec{b}\) maka \(a_1=b_1\), \(a_2=b_2\), dan
\(a_3=b_3\).
Baca Juga : SPLTV Metode Substitusi
Perbandingan Vektor
Perbandingan vektor terbagi menjadi dua bagian yaitu perbandingan
dalam bentuk koordinat dan perbandingan dalam bentuk vektor.
Perbandingan dalam Bentuk Koordinat
\(\overrightarrow{AB}:\overrightarrow{PB}= m:n\)
Untuk mencari koordinat titik \(P\), jika titik \(A\) dan \(B\)
serta perbandingannya diketahui maka kita akan menggunakan rumus
\(x_p=\frac{mx_b+nx_a}{m+n}\) dan \(y_p=\frac{my_b+ny_a}{m+n}\)
Contoh soal perbandingan dalam bentuk koordinat
Soal 1
Diketahui koordinat titik \(A(-2,1)\) dan \(B(8,-4)\). Jika
\(\overrightarrow{AP}:\overrightarrow{PB}=3:2\). Tentukan koordinat
titik \(P\)
Pembahasan
Dari soal di atas didapatkan nilai \(m=3\) dan \(n=2\).
Kita gambarkan dulu, agar lebih mudah dalam mengerjakannya.
Mencari nilai \(x_p=\)
\(x_p=\frac{mx_b+nx_a}{m+n}\)
\(x_p=\frac{3\times8+2\times(-2)}{3+2}\)
\(x_p=\frac{24-4}{5}\)
\(x_p=\frac{20}{5}\)
\(x_p=4\)
Mencari nilai \(y_p=\)
\(y_p=\frac{my_b+ny_a}{m+n}\)
\(y_p=\frac{3\times(-4)+2\times1}{3+2}\)
\(y_p=\frac{-12+2}{5}\)
\(y_p=\frac{-10}{5}\)
\(y_p=-2\)
Jadi diperoleh koordinat titik \(P\) adalah \((4,-2)\)
Soal 2
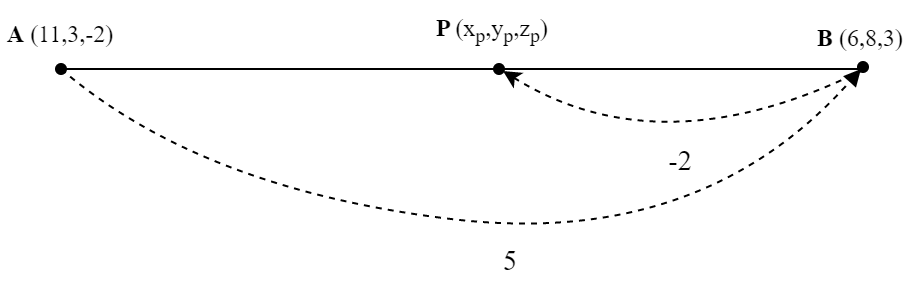
Titik \(P\) terletak pada garis AB. Koordinat titik \(A(11,3,-2)\) dan
titik \(B(6,8,3)\). Jika \(\overrightarrow{AB}:
\overrightarrow{BP}=5:-2\). Tentukan koordinat titik P.
Pembahasan
Pada soal ini perbandingan titik koordinatnya ada yang bernilai
negatif. Pada materi kesamaan vektor sudah saya terangkan
mengenai hal ini, jadi jika di depan vektor ada tanda
negatif maka arah vektornya
berlawanan dari arah vektor yang sesungguhnya.
Agar kita bisa mengerjakan soal ini menggunakan rumus
\(y_p=\frac{my_b+ny_a}{m+n}\) maka kita perlu mengubah perbandingan
dari \(\overrightarrow{AB}: \overrightarrow{BP}\) menjadi
\(\overrightarrow{AP}: \overrightarrow{PB}\).
Pada soal diketahui \(\overrightarrow{AB}: \overrightarrow{BP}=5:-2\).
Coba perhatikan gambarnya jarak \(A\) ke \(B\) \(= 5\) dan jarak \(B\)
ke \(P\) \(=-2\) berarti kalo jarak \(P\) ke \(B\) \(=2\) tinggal
dibalik aja dan nilainya juga berubah menjadi
kebalikannya.
Maka untuk mencari \(AP=AB-PB\).
\(AP=AB-PB\)
\(AP=5-2\)
\(AP=3\)
Mencari nilai \(x_p\)
\(x_p=\frac{mx_b+nx_a}{m+n}\)
\(x_p=\frac{3\times6+2\times11}{3+2}\)
\(x_p=\frac{18+22}{5}\)
\(x_p=\frac{40}{5}\)
\(x_p=8\)
Mencari nilai \(y_p\)
\(y_p=\frac{my_b+ny_a}{m+n}\)
\(y_p=\frac{3\times8+2\times3}{3+2}\)
\(y_p=\frac{24+6}{5}\)
\(y_p=\frac{30}{5}\)
\(y_p=6\)
Mencari nilai \(z_p\)
\(z_p=\frac{mz_b+nz_a}{m+n}\)
\(z_p=\frac{3\times3+2\times(-2)}{3+2}\)
\(z_p=\frac{9-4}{5}\)
\(z_p=\frac{5}{5}\)
\(z_p=1\)
Jadi Titik Koordinat \(P\) nya adalah \((8,6,1)\)
Perbandingan dalam Bentuk Vektor
Rumus perbandingan dalam bentuk vektor :
\[\vec{p}=\frac{m\vec{b}+n\vec{a}} {m+n}\]
Contoh soal perbandingan dalam bentuk vektor
Soal 1
Pehatikan gambar di bawah ini :
Jika \(\overrightarrow{AB}=\vec{u}\) dan
\(\overrightarrow{AD}=\vec{v}\). Nyatakanlah vektor
\(\overrightarrow{AE}\) dalam vektor \(\vec{u}\) dan
\(\vec{v}\).
Pembahasan
\(\overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{BC} =
\vec{u}+\vec{v}\)
\(\overrightarrow{AE}=
\frac{3\overrightarrow{AC}+5\overrightarrow{AD}}{3+5}= \frac
{3(\vec{u}+\vec{v})+5(\vec{v})}{8}= \frac
{3\vec{u}+3\vec{v}+5\vec{v}}{8}\)
\(\overrightarrow{AE}= \frac {3\vec{u}+8\vec{v}}{8}\)
Panjang Proyeksi dan Proyeksi Skalar
Panjang Proyeksi
Rumus panjang proyeksi :
Panjang proyeksi \(\vec{a}\) pada \(\vec{b}\)
Panjang proyeksi \(= \begin
{vmatrix}\frac{\vec{a}.\vec{b}}{\begin{vmatrix}\vec{b}\end{vmatrix}}
\end{vmatrix}\)
Panjang proyeksi \(\vec{b}\) pada \(\vec{a}\)
Panjang proyeksi \(= \begin
{vmatrix}\frac{\vec{a}.\vec{b}}{\begin{vmatrix}\vec{a}\end{vmatrix}}
\end{vmatrix}\)
Contoh soal panjang proyeksi
Diketahui \(A(-3,0,0)\), \(B(0,3,0)\) dan \(C(0,0,2)\). Tentukan
panjang proyeksi \(\overrightarrow{AC}\) pada \(\overrightarrow{AB}\).
Pembahasan
\(\overrightarrow{AB}= B-A\)
\(\overrightarrow{AB}= \begin{pmatrix}0\\3\\0\end{pmatrix}-
\begin{pmatrix}-3\\0\\0\end{pmatrix}\)
\(\overrightarrow{AB}= \begin{pmatrix}3\\3\\0\end{pmatrix}\)
\(\overrightarrow{AC}= C-A\)
\(\overrightarrow{AC}= \begin{pmatrix}0\\0\\2\end{pmatrix}-
\begin{pmatrix}-3\\0\\0\end{pmatrix}\)
\(\overrightarrow{AC}= \begin{pmatrix}3\\0\\2\end{pmatrix}\)
Mencari panjang vektor \(\overrightarrow{AB}\)
\(\begin{vmatrix}\overrightarrow{AB}\end{vmatrix}=\sqrt{3^{2}+3^{2}+0^{2}}\)
\(\begin{vmatrix}\overrightarrow{AB}\end{vmatrix}=\sqrt{9+9+0}\)
\(\begin{vmatrix}\overrightarrow{AB}\end{vmatrix}=\sqrt{18}\)
\(\begin{vmatrix}\overrightarrow{AB}\end{vmatrix}=3\sqrt{2}\)
Mencari panjang proyeksi \(\overrightarrow{AC}\) pada
\(\overrightarrow{AB}\)
Panjang proyeksi \(= \begin
{vmatrix}\frac{\overrightarrow{AB}.\overrightarrow{AC}}{\begin{vmatrix}\overrightarrow{AB}\end{vmatrix}}
\end{vmatrix}\)
Panjang proyeksi \(= \begin
{vmatrix}\frac{\begin{pmatrix}3\\3\\0\end{pmatrix}.
\begin{pmatrix}3\\0\\2\end{pmatrix}}{\begin{vmatrix}3\sqrt{2}\end{vmatrix}}
\end{vmatrix}\)
Panjang proyeksi \(= \begin {vmatrix}\frac{9+0+0}{3\sqrt{2}}
\end{vmatrix}\)
Panjang proyeksi \(= \begin {vmatrix}\frac{9}{3\sqrt{2}}
\end{vmatrix}\)
Panjang proyeksi \(= \begin {vmatrix}\frac{3}{\sqrt{2}}
\end{vmatrix}\)
Panjang proyeksi \(= \begin {vmatrix}\frac{3}{2}\sqrt{2}
\end{vmatrix}\)
Panjang proyeksi \(= \frac{3}{2}\sqrt{2}\)
Proyeksi Skalar
Rumus proyeksi skalar
Proyeksi skalar \(\vec{a}\) pada \(\vec{b}\)
\[=\frac{\vec{a}.\vec{b}}{\begin{vmatrix}\vec{b}\end{vmatrix}}\]Proyeksi skalar \(\vec{b}\) pada \(\vec{a}\)\[=\frac{\vec{a}.\vec{b}}{\begin{vmatrix}\vec{a}\end{vmatrix}}\]
Contoh soal proyeksi skalar
Diketahui \(\vec{a}=2i-2pj+4k\) dan \(\vec{b}= i-3j+4k\). Jika proyeksi
skalar vektor \(\vec{a}\) pada \(\vec{b}\) adalah
\(\frac{12}{\sqrt{26}}\), maka nilai \(p=....\)
Pembahasan
Diketahui :
Proyeksi skalar
\(=\frac{\vec{a}.\vec{b}}{\begin{vmatrix}\vec{b}\end{vmatrix}}\)
\(\frac{12}{\sqrt{26}}=\frac{\vec{a}.\vec{b}}{\begin{vmatrix}\vec{b}\end{vmatrix}}\)
Mencari nilai \(\vec{a}.\vec{b}\) :
\(\vec{a}.\vec{b}=
\begin{pmatrix}2\\-2p\\4\end{pmatrix}.\begin{pmatrix}1\\-3\\4\end{pmatrix}=\begin{pmatrix}2\\6p\\16\end{pmatrix}\)
Mencari nilai \(\begin{vmatrix}\vec{b}\end{vmatrix}\) :
\(\begin{vmatrix}\vec{b}\end{vmatrix}= \sqrt {1^{2}+(-3)^{2}+4^{2}}\)
\(\begin{vmatrix}\vec{b}\end{vmatrix}= \sqrt {1+9+16}\)
\(\begin{vmatrix}\vec{b}\end{vmatrix}= \sqrt {26}\)
Mencari nilai \(p\)
\(\frac{12}{\sqrt{26}}=\frac{\vec{a}.\vec{b}}{\begin{vmatrix}\vec{b}\end{vmatrix}}\)
\(\frac{12}{\sqrt{26}}=\frac{2+6p+16}{\sqrt {26}}\)
\(\frac{12}{\sqrt{26}}=\frac{6p+18}{\sqrt {26}}\)
\(12=6p+18\)
\(p = -1\)
Vektor Proyeksi
Rumus Vektor Proyeksi
Vektor proyeksi \(\vec{a}\) pada \(\vec{b}\)
\[\frac{\vec{a}.\vec{b}}{\begin{vmatrix}\vec{b}\end{vmatrix}^{2}}.\vec{b}\]Vektor proyeksi \(\vec{b}\) pada \(\vec{a}\)\[\frac{\vec{a}.\vec{b}}{\begin{vmatrix}\vec{a}\end{vmatrix}^{2}}.\vec{a}\]
Contoh Soal Vektor Proyeksi
Diketahui vektor \(\vec{a}=4i-2j+2k\) dan vektor \(\vec{b}=2i-6j+4k\).
Proyeksi orthogonal vektor \(\vec{a}\) pada vektor \(\vec{b}\)
adalah....
Pembahasan
Mencari nilai \(ab\) :
\(ab =
\begin{pmatrix}4\\-2\\2\end{pmatrix}.\begin{pmatrix}2\\-6\\4\end{pmatrix}\)
\(8+12+8=28\)
Mencari nilai \(\begin{vmatrix}\vec{b}\end{vmatrix}\) :
\(\begin{vmatrix}\vec{b}\end{vmatrix}=\sqrt{2^{2}+(-6)^{2}+4^{2}}\)
\(\begin{vmatrix}\vec{b}\end{vmatrix}=\sqrt{4+36+16}\)
\(\begin{vmatrix}\vec{b}\end{vmatrix}=\sqrt{56}\)
Mencari proyeksi vektor \(\vec{a}\) pada \(\vec{b}\) :
\(\frac{\vec{a}.\vec{b}}{\begin{vmatrix}\vec{b}\end{vmatrix}^{2}}.\vec{b}=\)
\(\frac{28}{(\sqrt{56})^{2}}.\begin{pmatrix}2\\-6\\4\end{pmatrix}=\)
\(\frac{28}{56}\begin{pmatrix}2\\-6\\4\end{pmatrix}=\)
\(\frac{1}{2}.\begin{pmatrix}2\\-6\\4\end{pmatrix}=\begin{pmatrix}1\\-3\\2\end{pmatrix}
\)
Perkalian Titik Dua Buah Vektor atau Dot Product, Jika Besar Sudutnya Diketahui
Rumusnya :
\[\vec{a}.\vec{b}=\begin{vmatrix}\vec{a}\end{vmatrix}.\begin{vmatrix}\vec{b}\end{vmatrix}cos \hspace{1mm}\theta\]
Dengan \(0\leq\theta\leq\pi\) artinya \(\theta\) selalu berada di
kuadran \(1\).
Contoh Soal Perkalian Titik Dua Buah Vektor, Jika Besar Sudut Antara Dua Vektor Diketahui
Jika sudut antara \(\vec{a}=i+\sqrt{2}j+pk\) dan
\(\vec{b}=i-\sqrt{2}j+pk\) adalah \(60^{\circ}\), maka \(p=...\)
Pembahasan
Mencari nilai \(\vec{a}\vec{b}\) :
\(\vec{a}\vec{b}=\begin{pmatrix}1\\ \sqrt{2}\\
p\end{pmatrix}.\begin{pmatrix}1\\-\sqrt{2}\\p\end{pmatrix}\)
\(\vec{a}\vec{b}= 1-2+p^{2}\)
\(\vec{a}\vec{b}= p^{2}-1\)
Mencari nilai
\(\begin{vmatrix}\vec{a}\end{vmatrix}\begin{vmatrix}\vec{b}\end{vmatrix}\)
\(\begin{vmatrix}\vec{a}\end{vmatrix} = \sqrt
{1^{2}+(\sqrt{2})^{2}+p^{2}}\)
\(\begin{vmatrix}\vec{a}\end{vmatrix} = \sqrt {1+2+p^{2}}\)
\(\begin{vmatrix}\vec{a}\end{vmatrix} = \sqrt {3+p^{2}}\)
\(\begin{vmatrix}\vec{b}\end{vmatrix} = \sqrt
{1^{2}+(-\sqrt{2})^{2}+p^{2}}\)
\(\begin{vmatrix}\vec{b}\end{vmatrix} = \sqrt {1+2+p^{2}}\)
\(\begin{vmatrix}\vec{b}\end{vmatrix} = \sqrt {3+p^{2}}\)
\(\begin{vmatrix}\vec{a}\end{vmatrix}\begin{vmatrix}\vec{b}\end{vmatrix}=\sqrt
{3+p^{2}}.\sqrt {3+p^{2}}\)
\(\begin{vmatrix}\vec{a}\end{vmatrix}\begin{vmatrix}\vec{b}\end{vmatrix}=3+p^{2}\)
Mencari nilai \(cos \hspace{1mm}60^{\circ}\)
\(cos \hspace{1mm}60^{\circ}=\frac{1}{2}\)
Mencari nilai \(p\)
\(cos\hspace{1mm}60^{\circ}=\frac{\vec{a}\vec{b}}{\begin{vmatrix}\vec{a}\end{vmatrix}\begin{vmatrix}\vec{b}\end{vmatrix}}\)
\(\frac{1}{2}=\frac{p^{2}-1}{3+p^{2}}\)
\(3+p^{2}=2p^{2}-2\)
\(p^{2}=5\)
\(p=\pm\sqrt{5}\)
Penutup
Sekian rangkuman materi vektor matematika pdf, semoga bermanfaat dan
jangan lupa share ke teman-temannya. Apabila ada yang tidak mengerti
atau kesalahan penulisan dari artikel ini silahkan ditanyakan.
Terimakasih......